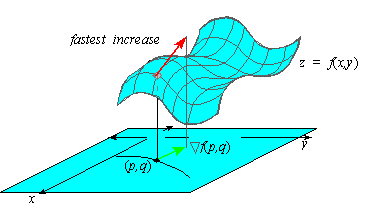
Properties of the Gradient   

If we let q denote the angle between Ñf and a given unit vector u, then

Duf = || Ñf||  || u|| cos( q) = || Ñf||  cos( q)

since || u|| = 1. Thus, the directional derivative is largest when q = 0, which is in the direction of Ñf, and is smallest when q = p, which is in the direction of -Ñf.  

 

Theorem 7.2: The slope ( D_uf) ( p) of the tangent line to a vertical slice of z = f(x,y) through ( p,q,f( p) ) is greatest in the direction of Ñf( p) and is smallest in the direction of -Ñf( p) .

We say that Ñf( p,q) is the direction of steepest ascent for the surface z = f( x,y) at (p,q) . Analogously, -Ñf( p,q) must the direction of steepest descent or direction of least resistance at the point ( p,q) .

Moreover, when u is the direction vector for Ñf, then u = Ñf/||Ñf||, so that

Duf  =  Ñf ·  Ñf ||Ñf||  =   ||Ñf||2 ||Ñf||  =  ||Ñf||

Similarly, if u is in the direction of -Ñf, then D_uf = -||Ñf||. Also, the corresponding tangent vectors to the surface are

fastest increase : vinc =  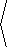fx ||Ñf|| ,  fy ||Ñf|| ,||Ñf|| 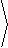fastest decrease : vdec = - fx ||Ñf|| , -fy ||Ñf|| ,-||Ñf||

This is important in many numerical routines.

LiveGraphics3d Applet

EXAMPLE 4    How fast is f( x,y) = x²+y³ increasing at ( 2,1) when it is increasing the fastest?       

Solution: To begin with, Ñf = á2x,3y² ñ . Moreover, f is increasing the fastest when u is in the direction of Ñf( 2,3) = á4,3 ñ , and in this direction, we have

( Duf) ( 2,1) = || á4,3 ñ || = 5

(The notation ( D_uf) ( p,q) means the directional derivative D_uf evaluated at the point (p,q) . )

Moreover, given a collection of increasing constants k₁ < k₂ < k₃ < ¼, the set of level curves

f( x,y) = k1,    f( x,y) = k2,    f(x,y) = k3,    and so on

forms a family of level curves in the xy-plane in which the levels are increasing. It then follows that Ñf( p,q) points in the direction in which the levels are increasing the fastest, and -Ñf( p,q) points in the direction in which the levels are decreasing the fastest.

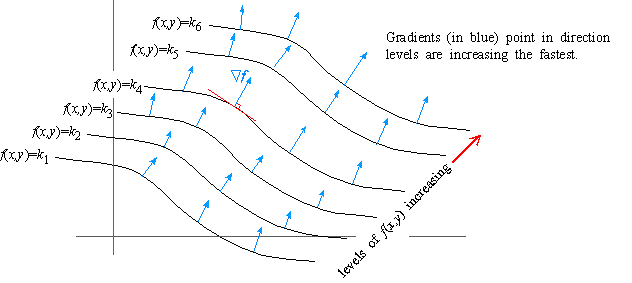
EXAMPLE 5    In what direction are the levels of f(x,y) = x³y increasing the fastest at the point ( 2,3) ?       

Solution: The levels of f are increasing the fastest in the direction of Ñf( 2,3) . Since Ñf = á3x²y,x³ ñ , we have Ñf( 2,3) = á 36,8 ñ . Thus, the levels of f are increasing the fastest in the direction

u =   Ñf( 2,3) || Ñf(2,3) ||  =    á 36,8 ñ || á 36,8 ñ ||  =   9 85 ,  2 85