Gradients and Level Curves
In this section, we use the gradient and the chain rule to
investigate horizontal and vertical slices of a surface of the form z = g( x,y) . To begin with, if k is constant, then g(x,y) = k is called the level curve of g( x,y) of
level k and is the intersection of the horizontal plane z = k and the
surface z = g( x,y) :
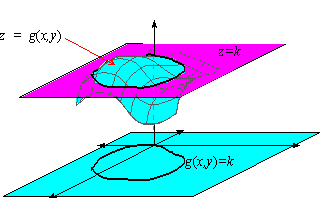
In particular, g( x,y) = k is a curve in the xy-plane.
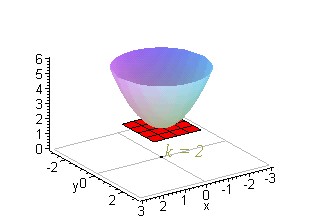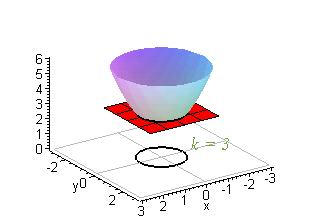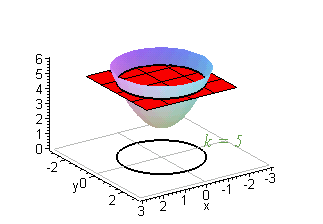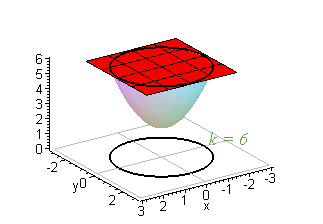
EXAMPLE 1 Construct the level curves of g( x,y) = x2+y2+2 for k = 2,3,4,5, and 6.
Solution: To begin with, g( x,y) = k is of the form x2+y2+2 = k, which simplifies to
If k = 2, then x2+y2 = 0 which is true only if ( x,y) = ( 0,0) . For k = 3,4,5,and 6, we have
These are circles centered at ( 0,0) with radii 1,Ö2,Ö3, and 2, respectively.
If g( x,y) is differentiable, then the level curve g( x,y) = k can be parametrized by a vector-valued function of
the form r( t) =
á x( t) ,y(t)
ñ . If v denotes the velocity of r, then the chain
rule implies that
|
|
d
dt
|
g( x,y) = |
d
dt
|
k Þ Ñg·v = 0 |
|
Thus, Ñg is perpendicular to the tangent line to g(x,y) = k at the point ( p,q) .
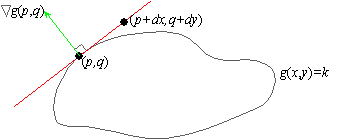
We say that Ñg( p,q) is normal to the curve g( x,y) = k at ( p,q) .
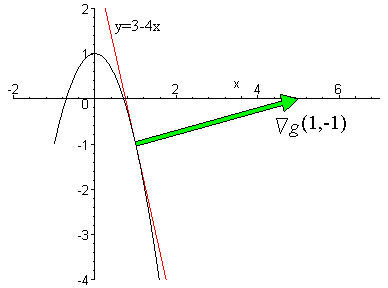
EXAMPLE 2 Show that the gradient is normal to the curve y = 1-2x2 at the point ( 1,-1) .
Solution: To do so, we notice that 2x2+y = 1. Thus, the curve is
of the form g( x,y) = 1 where g( x,y) = 2x2+y.
The gradient of g is
Thus, at ( 1,-1) , we have Ñg( 1,-1) =
á 4,1
ñ . However, if y = 1-2x2, then y' = -4x, and when x = 1, we have y'( 1) = -4. That is, a
run of 1 leads to a rise of -4, so that the slope corresponds to the
vector
|
m =
á run,rise
ñ =
á1,-4
ñ |
|
Clearly, Ñg·m =
á 4,1
ñ ·
á 1,-4
ñ = 0, thus implying that Ñg is
perpendicular to the tangent line to y = 1-2x2 at ( -1,1) .
Check Your Reading: Are there any level curves of g( x,y) = x2+y2+2 with a level lower than k = 2?




