The Chain Rule in Non-Vector Form

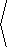
Ñf · v = á fx, fy ñ ·   dx dt , dy dt  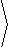   = fx  dx dt    +   fy  dy dt

The Chain Rule(non-vector form):  Suppose that x( t) and y( t) are differentiable at t₀ and that f(x,y) is differentiable at ( x( t₀) ,y(t₀) ) .  If w = f(x,y) , then w( t) is differentiable at t₀ and

w' (t0)    =    ¶f ¶x   dx dt   +  ¶f ¶y   dy dt

Equivalently, the chain rule produces the same derivative dw/dt that we would obtain directly by substituting for x and y in f(x,y) and differentiating with respect to t.       

EXAMPLE 3    Find dw/dt given that w = x²+y³ and that x = t³, y = t⁵.

  Solution: The first partial derivatives of w = x²+y³ are

¶w ¶x = 2x,         ¶w ¶y = 3y2

As a result, the chain rule says that

dw dt   = 2x  dx dt +3y2  dy dt   = 2x( 3t2) + 3y2( 5t4) = 2t3( 3t2) + 3t10( 5t4) = 6t5 + 15t14

Notice that we would have obtained the same result if we had substituted

w = ( t3 )2 + ( t5 )3 =  t6 + t15

and then calculated dw/dt.

   

Likewise, if w = f( x,y,z) where x, y, and z are functions of t, then

dw dt = ¶f ¶x   dx dt  + ¶f ¶y   dy dt  + ¶f ¶z   dz dt

if x and y are differentiable at t₀ and f( x,y) is differentiable at ( x( t₀) ,y( t₀) ).    

EXAMPLE 4    Find dw/dt given that w = cos( xy) +z and that x = pe^t, y = e^-t, and z = t²

Solution: The first partial derivatives are

¶w ¶x = -ysin( xy) ,    ¶w ¶y = -xsin( xy) ,    ¶w ¶z = 1

As a result, the chain rule says that

dw dt = -ysin(xy)  dx dt  - xsin(xy) dy dt  + dz dt

and since dx/dt = pe^t,   dy/dt = -e^-t, and dz/dt = 2t, we have

dw dt   = = -e-tsin( pete-t) ( pet) -petsin( pete-t) (-e-t) +2t = -pete-tsin( pete-t) +pete-tsin( pete-t ) +2t = -psin(p) +psin(p) +2t = 2t

Check your Reading: : Substitute x = pe^t , y = e^-t, and z = t² into w = cos( xy) +z to reveal another reason why we should have dw/dt = 2t in example 4.