Exercises

Each of the limits shown below does exist. Estimate its value intuitively, if possible, and then use a table to estimate the limit. Be sure to use radians when trigonometric functions are involved.
1.

lim
( x,y) ® ( 2,3)  
 xy
2.

lim
( x,y) ® ( 3,4)  
 (x2+y2)
3.

lim
( x,y) ® ( 2,p)  
 xcos(y)
4.

lim
( x,y) ® ( p,2)  
 sin( xy)
5.

lim
( x,y) ® ( 2,1)  
  x2y2-x2-4y2+4
yx-x-2y+2
6.

lim
( x,y)® ( 2,1)  
  x2y-x2-4y+4
xy2-x-2y2+2
7.

lim
( x,y) ® ( p,0)  
  cos( x-y) -cos( x+y)
sin( x+y) +sin( x-y)
8.

lim
( x,y) ® (p/2,p)  
  cos( x-y) +cos( x+y)
sin( x+y) +sin( x-y)
9.

lim
( x,y) ® ( 0,0)  
  sin( x2+y2)
x2+y2
10.

lim
(x,y) ® ( 0,0)  
  sin(x2+y2)
x+y

Show that the following limits do not exist by evaluating the limit along two different paths which produce 2 different results.
11.

lim
( x,y) ® ( 0,0)  
  x-y
x+y
12.

lim
( x,y) ® ( 0,0)  
  x+4y
x+y
13.

lim
( x,y) ® ( 0,0)  
  x2-y2
x2+y2
14.

lim
( x,y) ®( 0,0)  
  x3-y3
x2-y2
15.

lim
( x,y) ® ( 0,0)  
  2xy
x2+y2
16.

lim
( x,y) ® (0,0)  
  4xy
x2+y2
17.

lim
( x,y) ® ( 0,0)  
  xy2
x2+y4
18.

lim
( x,y) ® (0,0)  
  x2y+xy2
x4+y4
19.

lim
( x,y) ® ( 0,0)  
  x3+y3
x3+y2
20.

lim
( x,y) ®( 0,0)  
  x3-y3
x2-y2
21.

lim
( x,y) ® ( p,0)  
  sin( x)
x+y-p
22.

lim
( x,y) ®( 0,0)  
  sin( x)
x+y

Determine where the following functions are continuous.
23.
f( x,y) =  x+y
x-y
24.
f( x,y) =  x+y
x+4y
25.
f( x,y) = ln( x) sec( y)
26.
f( x,y) =  ln( x)
ln( |x-y| )
27.
f( x,y) = ln( 1-x2-y2)
28.
f( x,y) = tan-1 æ
è 		 y
x
 ö
ø

           

29. Evaluate the limit

lim
( x,y) ® ( 2,1)  
  x2y2-x2-4y2+4
yx-x-2y+2
by factoring the numerator and the denominator to obtain the limit of function which is continuous at ( 2,1) .

30. Evaluate the limit

lim
( x,y) ® ( p,0)  
  cos(x-y) -cos( x+y)
sin( x+y) +sin(x-y)
by simplifying the numerator and denominator to obtain the limit of a function which is continuous at ( p,0) .

31. Prove the following: If g( x) is continuous at x = p, then f( x,y) = g( x) is continuous at ( p,y) for all real numbers y.

32. In example 5, we showed that the limit

lim
( x,y) ® ( 0,0)  
  x2y
x4+y2
does not exist by showing that it has a value of 0 along any line through the origin, but that it has a limit of 1/2 along the curve y = x2. Use a table to explore this limit. How would you choose the x's and y's so as to reveal the limit of 1/2 along the curve y = x2?

33. What is the domain of the function
f( x,y) =  x
y
 sin æ
è 		 y
x
 ö
ø
Then determine if the following limit exists:

lim
( x,y) ® ( 0,0)  
 f( x,y)

34. Let us define
f( x,y) = ì
í
î
0
if
x = y
x-y
if
x ¹ y
Determine if the following limit exists:

lim
( x,y) ® ( 0,0)  
 f( x,y)
Where is f continuous?

35. Use the definition of the limit to prove that if

lim
( x,y) ® ( p,q)  
 f( x,y) = L
and if k is a number, then

lim
( x,y) ® ( p,q)  
 kf( x,y) = kL

36. Use the definition of the limit to prove that if

lim
( x,y) ® ( p,q)  
 f( x,y) = L        and       
lim
( x,y) ® (p,q)  
 g( x,y) = K
then the limit of the sum exists and

lim
( x,y) ® ( p,q)  
 [ f(x,y) +g( x,y) ] = L+K

37. Write to Learn: In a short essay, explain why

lim
( x,y) ® ( 0,0)  
  x-1
x+y
    d.n.e    and       
lim
( x,y) ® (0,0)  
  y+1
x+y
   d.n.e
where ``d.n.e.'' means ``does not exist.'' Then conclude the essay by using these two limits to show that

lim
( x,y) ® ( p,q)  
 [ f(x,y) +g( x,y) ]
may exist even when the individual limits of the summand do not exist.

38. Write to Learn: A polygonal path is a piecewise linear curve with vertices
( x1,y1) ,( x2,y2) ,¼,(xn,yn) ,¼
where xn approaches p and yn approaches q.

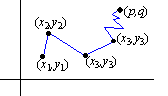
Write a short essay explaining why if

lim
n® ¥ 
 f( xn,yn) = L
for every polygonal path to ( p,q) , then the limit of f(x,y) as ( x,y) approaches ( p,q) exists and

lim
( x.y) ® ( p,q)  
 f( x,y) = L

39. In this exercise, we show that the norm ||x||  as a function of x  is a continuous function.  

    1. Explain why 2x·p £ 2||x||||p|| (i.e., how big can the cosine of an angle get), and then use it to explain why  

      | | x| | 2-2|| p| |  | | x| | +| | p|| 2 £ | | x| |2-2p·x+| | p|| 2

      2.  

    2. Factor both sides of the inequality in (a) and apply the square root to show that

      |  | | x| |-| | p| |  | £ | | x-p| |

      3.  

    3. Use (b) and the definition of the limit to prove that

       
      lim
      x® p 
      		 ||x|| = ||p||

40.  Let us suppose that we define
f( x) =  1
||x||
  x
Show that the limit of f( x) as x approaches 0 does not exist.