Part 4:  Torsion and the Frenet Frame   

Given a curve r(t) in space, the binormal vector B is defined

B = T×N

Thus, B is a unit vector normal to the plane spanned by T and N at time t.  The 3 vectors T, N, and B taken together are called either the TNB frame or the Frenet Frame of the curve.

click to toggle animation

Since both v and a are in the plane spanned by T and N, the binormal vector B is also the unit vector in the direction of v×a.  That is,

B =  v×a || v×a||

Moreover, if B is constant, then the curve r(t) must be contained in a plane with normal B.      

EXAMPLE 6    Find B for r( t) = á sin( t), -cos( t), sin(t) ñ . Is r( t) in a plane?      

Solution: Since v(t) = á cos(t), sin(t), cos(t) ñ and a(t)  =   á -sin(t), cos(t), -sin( t) ñ , their cross product is

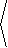
v×a = ê ê ê sin( t) cos( t) cos( t) -sin( t) ê ê ê , ê ê ê cos( t) cos( t) -sin( t) -sin( t) ê ê ê , ê ê ê cos( t) sin( t) -sin( t) cos( t) ê ê ê

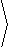
which simplifies to

v×a = á -sin2( t) - cos2(t), 0, cos2( t) + sin2( t) ñ = á -1,0, 1 ñ

Since || v×a|| = Ö2, the unit binormal is

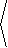
B =   -1 2 ,0, 1 2

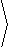
Moreover, B is constant, so r( t) is confined to a single plane, as is shown below:

Frenet Frame

Finally, the definition B = T×N implies that

dB dt  =  dT dt ×N + T× dN dt

However, dT/dt is parallel to N, so that dT/dt×N = 0 and

dB dt   =  T× dN dt

Thus, dB/dt must be perpendicular to T. Moreover, the fact that B( t) is a unit vector for all t implies that dB/dt is also perpendicular to B. Thus, dB/dt is parallel to N, which means that

dB dt   = -t  vN

(11)

where the constant of proportionality t is known as the torsion of the curve. It follows that

t = - 1 v N· dB dt

Torsion is a measure of how much the plane spanned by T and N "osculates" as the parameter increases.  For example, if r(t) is a curve contained in a single fixed plane, then B must be constant and consequently, the torsion t = 0.  In fact, t = 0 only if motion is in a plane.  More properties of t  will be explored in the exercises.