Part 4: Plane of Motion and Maximum Altitude   

Let's suppose that r( t) is the position of a projectile at time t. Since v and a always lie in the same plane, the motion of the projectile is in the plane through the point r₀ with normal

n = v0×a

The maximum altitude occurs when v is horizontal, which is when the 3rd component of v is identically zero. The time to maximum altitude is denoted t_max and is obtained by setting the third component of v equal to 0 and solving for t.

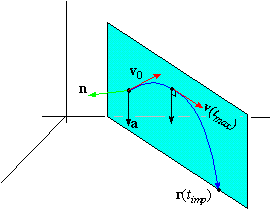
Finally, the point at which the projectile ``strikes'' the ground (i.e., the xy-plane) is the point at which the third component of r(t) is equal to 0. Setting the third component of r(t) equal to 0 and solving for t thus yields the time of impact, denoted t_imp. The point of impact is r(t_imp) .      

EXAMPLE 7    Suppose a projectile has a position at time t of

r( t) = á 10t,20t,64t-16t2 ñ

Find the plane of motion, the time to maximum height, the maximum height, the time of impact, and the point of impact of the projectile.               

Solution: To begin with, the velocity of the object is

v( t) = á 10,20,64-32t ñ

and the acceleration is as expected, a( t) = á 0,0,-32 ñ . Since

n = v0×a = á10, 20, 64 ñ × á 0,0,-32 ñ =  á - 640, 320, 0 ñ

the plane of motion is the plane through r₀ = ( 0,0,0) with normal n = á -640,320,0 ñ . Thus, the equation of the plane of motion is

-640( x-0)  + 320( y-0) + 0( z-0) = 0

which is the vertical plane passing through the line y = 2x. 

To find t_max, we set the third component of v(t) equal to 0 and solve for t_max.

64-32t  =   0 32t  =   64 tmax  =   2

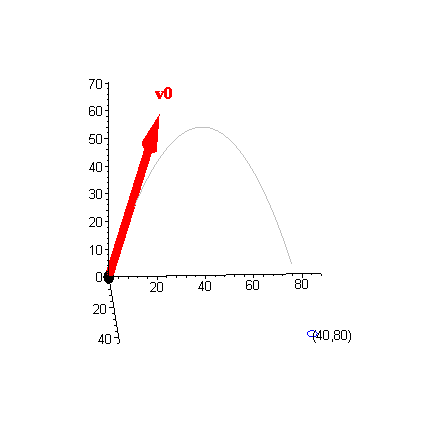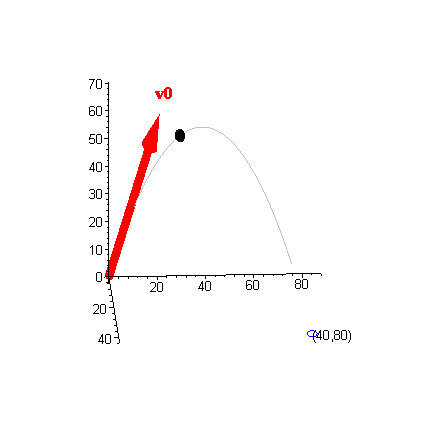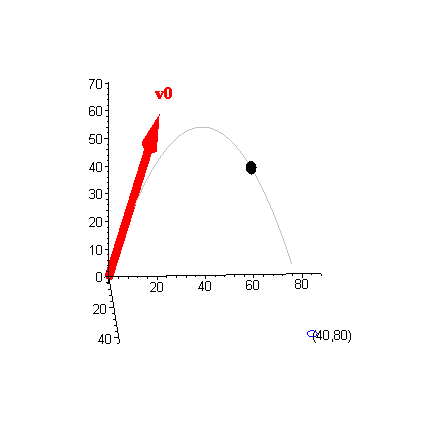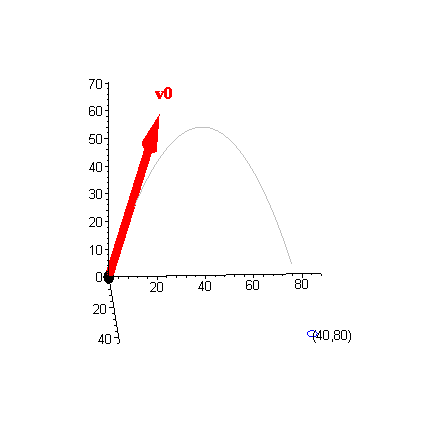
Since t_max = 2, the maximum altitude itself is simply the z-coordinate of r( t_max) . Since

r( tmax) = r( 2) = á20,40,128-64 ñ = á 20,40,64 ñ

the maximum altitude of the projectile is 64 feet. Finally, the time of impact occurs when the third component of r( t) is equal to 0:

64t-16t2  =  0 16t( t-4)  =  0 t  =  0  or  t = 4

Initially, the projectile is on the ground (i.e., r₀ = á 0,0,0 ñ ). Thus, the time of impact must be t_imp = 4, so that the point of impact is

r( timp) = r( 4) = (40,80,0)

click to toggle animation