Part 1: Vector-Valued Functions

Now that we have introduced and developed the concept of a vector, we are ready to use vectors to define functions. To begin with, a vector-valued function is a function whose inputs are a parameter t and whose outputs are vectors r( t) .

In 2 dimensions, a vector-valued function is of the form

r( t) = á f( t) ,g( t) ñ

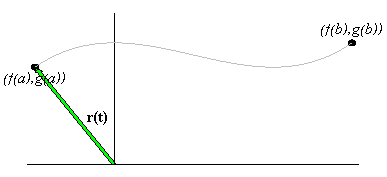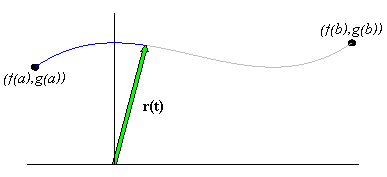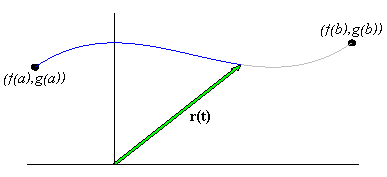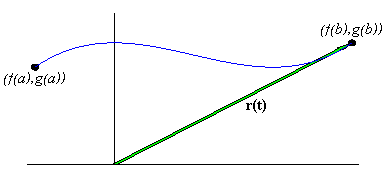
If f and g are continuous functions over [a,b], then the set of position vectors of the form r( t) = á f( t) ,g( t) ñ for t in [ a,b] forms a curve whose orientation is in the direction in which the parameter is increasing. The point r(a) = (f(a),g(a)) is called the initial point of the curve, and the point r(b) = (f(b),g(b))  is the curve's terminal point.

click image to toggle animation

The function r( t) = á f(t) ,g( t) ñ , t in [ a,b] , is called a parametrization of the curve.  To sketch the curve, we often let

x = f( t) ,        y = g( t) ,        t  in [ a,b]

and then eliminate the parameter t in hopes of obtaining a familiar equation in x and y.      

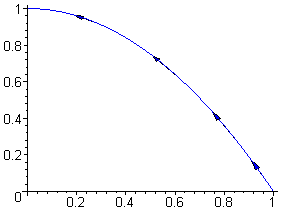
EXAMPLE 1    Sketch the curve parametrized by r(t) = á 1-t²,2t²-t⁴ ñ for t in [ 0,1] .       

Solution: To begin with, x = 1-t², which means that t² = 1-x. Since y = 2t²-t⁴, that means that

y = 2( 1-x) -( 1-x) 2

(1)

which simplifies to y = 1-x². Moreover, the initial and terminal points are

initial: ( t = 0) x = 1-02 = 1, y = 2·0-04 = 0 terminal: ( t = 1) x = 1-12 = 0, y = 2·1-14 = 1

That is, the graph of r( t) = á1-t²,2t²-t⁴ ñ for t in [ 0,1] is the section of the graph of y = 1-x² between the initial point (1,0) and the terminal point ( 0,1) .

       

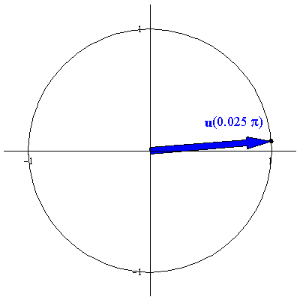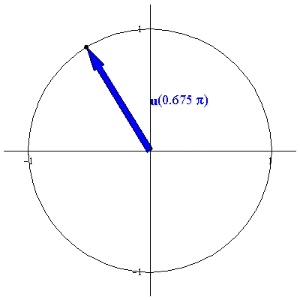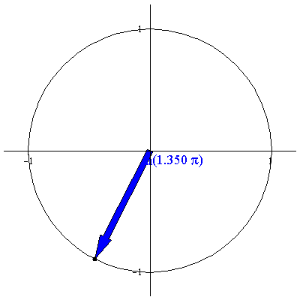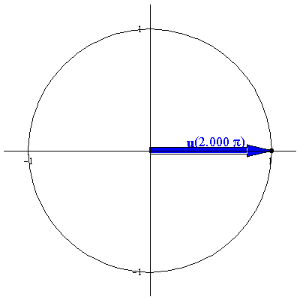
EXAMPLE 2    Sketch the curve parameterized by u(q) = á cos(q), sin(q) ñ for q in [ 0,2p] .       

Solution: Since x = cos(q) and y = sin(q), we begin with

cos2(q)  + sin2(q) = 1

Thus, the identity implies that

x2 + y2 = 1

which is the unit circle. Moreover, the initial and terminal points are

initial: ( q = 0) x = cos( 0) = 1, y = sin( 0) = 0 terminal: ( q = 2p) x = cos( 2p) = 1, y = sin( 2p) = 0

Since the initial and terminal points are both (1,0), we can determine the orientation of the circle by examining if an angle close to 0 produces a point above or below the unit circle. For example, u(p/4) is in the first quadrant, thus showing that the orientation of the curve is counterclockwise:

click to toggle animation

Example 2 is a revisitation of a fundamental idea in trigonometry, which is that the standard parameterization of the unit circle is given by

u(q) = á cos(q),  sin(q) ñ

where θ is in radians. The use of the letter "u" is because u(q)is a unit vector for each value of the angle q.