Exercises

Find the Cartesian equation in x and y of the graph of the given vector-valued function. Then sketch the graph showing orientation, if the orientation is well-defined.

1. r( t) = á t-1,t+1 ñ , 2. r( t) = át2,1-t4 ñ t in [ 0,1] t in [ 0,2] 3. r( t) = á t2,t3 ñ 4. r( t) = át3,t2 ñ t in [ 0,1] t in [ 0,1] 5. r( t) = át2+1,t2+2t ñ 6. r( t) = á t4+1,t2+2t ñ t in [ 0,1] t in [ 0,1] 7. r( t) = á 2cos( t),2sin( t) ñ 8. r( t) = á cosh( t) ,sinh( t) ñ t in [ 0,p] t in [ 0,1] 9. r( t) = á 2cos( t),3sin( t) ñ 10. r( t) = á 3sin( t) ,2cos( t) ñ t in [ 0,2p] t in [ 0,2p] 11. r( t) = á cos2( t),cos( 2t) ñ 12. r( t) = á tan( t) ,sec( t) ñ t in [ 0,p] t in é ë 0, p 4 ù û 13. r( t) = á 2cos( t)+1,sin( t) ñ 14. r(t) = á cos( t) ,sin2( 2t) ñ t in [ 0,2p] t in [ 0,1]

 

15. r( t) = á 1+sin( t),2+cos( t) ñ 16. r(t) = á 2-cos( t) ,4+sin( t) ñ t in [ 0,2p] t in [ 0,2p] 17. r( t) = á 1+sin2(t) ,2+3cos( t) ñ 18. r( t) = á 1+cos( t) ,( 2+cos( t) ) 2 ñ t in [ 0,2p] t in [ 0,p] 19. r( t) = á 3cos( 2t),2cos( t) ñ 20. r( t) = á et,e-t ñ t in [ 0,2p] t in [ 0,1] 21. r( q) = á 2cos2(q) ,2sin( q) cos( q) ñ 22. r( q) = á csc( q) ,sec( q) ñ q in [ 0,p] q in (0,p/2) 23. r( q) = cos(q) cos( q) +sin( q) , sin( q) cos( q) +sin(q) 24. r( q) = cos( q) 2-cos( q) , sin( q) 2-cos( q) q in -p 4 , 3p 4 q in [ 0,2p]

In exercises 25 - 28, parameterize in terms of q. In exercises 29 -32, parameterize the uniform circular motion using the given properties. Sketch the result.

25. Center: ( 1,1) , Radius = 3 26. Center: (-3,1) , Radius = 1 27. Center: ( 1,-3) , Radius = 5 28. Center: (-2,-5) , Radius = 0.1 29. Center: ( -4, -4)  , R = 3, w = 5  30. Center: (2, 3) , R = 0.1, w = 2 31. Center: ( 1,1) , Radius = 3 feet 32. Center: (1,2) , Radius = 5 feet T = 6 seconds,   t0 = 1 sec T = 2p seconds,    t0 = p sec

33. The curve below resembles something you might draw with a spirograph. Graph it with a graphing calculator or a computer for t in [ 0,10] .

r( t) = á cos( t) -cos(80t) sin( t) ,2sin( t) -sin(80t) ñ

34. The curve below resembles something you might draw with a spirograph. Graph it with a graphing calculator or a computer for t in [ 0,10] .

r( t) = á 10sin( t) +2cos(30t) ,12cos( 3t) +sin( 30t) ñ

35. Prove the following: If r( t) = á f( t) ,g( t) ñ , t in [ a,b] , is a parameterization of a curve C, then so also is

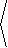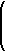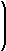
rk( t) =   f t k , g 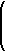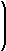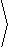t k , t in [ka,kb]

for every number k > 0.

36. Prove the following: If r( t) = á f( t) ,g( t) ñ , t in [ a,b] , is a parameterization of a curve C, then

r( t) = á f( -t) ,g( -t) ñ ,    t  in [ -b,-a]

is a parameterization of C with the opposite orientation.

37. The curve parameterized by r( t) = á t+1-sin( t) ,1-cos( t) ñ, t in [ 0,4p] , is an example of a Cycloid of Clairaut. Sketch it using a graphing calculator or a computer algebra system.

38. The curve parameterized by r( t) = á 2cos( t) +2cos²( t) ,2sin(t) +sin( 2t) ñ , t in [ 0,2p] , is called a cardoid. Sketch it using a graphing calculator or a computer algebra system.

39. The curve parameterized by r( t) = á cos³( t) ,sin³( t) ñ , t in [ 0,2p] , is called an astroid.

1. Sketch it using a graphing calculator or a computer algebra system.
2. Show that the equation of the astroid is

   | x| 2/3+| y| 2/3 = 1

40. The set of curves parameterized by r(t) = á ae^-t/10cos( t) ,be^-t/10sin(t) ñ , t in [ 0,8p] , for a and b constants is a family of spirals which spiral toward the origin.  

1. Sketch the curves corresponding to several values for a and b using a graphing calculator or a computer algebra system (or the "Tool" for this section).
2. Show that the curve satisfies the system of differential equations

   dx dt = -1 10 x-y,        x(0) = a dy dt = -1 10 y+x,        y( 0) = b

3. We say that the system of equations in (b) has a stable equilibrium at ( 0,0) . Use (a) to explain what this term means for this system of differential equations.

41. The earth orbits the sun in a nearly circular orbit with a period of 365.25 days and a radius of R = 93,000,000 miles. What is the parameterization of the earth's orbit about the sun? 

42. Even as you read this, you are moving in a circle as the earth rotates. The radius R of your circle of motion depends on your latitude, f, where

R = 3963 cos(f)    miles

Find out what your latitude is, use an angular velocity of 2p radians every 24 hours, and determine the parameterization for your approximate circle of motion.

43.  What is the parameterization of the circle in the animation shown below:

click to toggle animation

44. What is the angular speed of the circle in problem 43? 

45. Write to Learn: A Reuleaux Triangle is a curve formed by circular arcs connecting vertices of an equilateral triangle with sides of length r, where each arc is centered at a vertex of the triangle.
Write a short essay in which you present the parameterization of the Releaux triangle in a coordinate system with the origin at the center of the triangle and the y-axis passing through a vertex.

46.  Reuleaux triangles have many applications -- for example, drill bits for square holes and Mazda rotary engines (i.e., Wankel engines). Most applications are due to the fact that a Reuleaux triangle has a constant width, where constant width means that any two parallel lines intersecting the boundary of are the same distance apart. How "wide" is a Reuleaux triangle? Why is it of constant width?