Part 4: The Span of Two Non-parallel Vectors
A linear combination of non-parallel vectors u
and v is a vector of the form
where a and b are numbers. The set of all linear combinations of 2
non-parallel vectors u and v is called the span
of u and v.
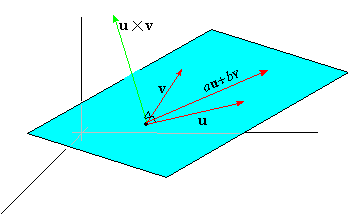
Moreover, if u and v are parallel to given plane P,
then the plane P is said to be spanned by u and v.
EXAMPLE 7 Find the equation of the plane through the point P1( 0,0,0) spanned by the vectors u =
á1,2,1
ñ and v =
á 3,1,-2
ñ
Solution: The normal to the plane is n = u×v, which is
|
n = u×v =
á 1,2,1
ñ ×
á 3,1,-2
ñ =
á -5,5,-5
ñ |
|
Definition 4.1 then implies that the equation of the plane is
|
-5( x-0) +5( y-0) -5( z-0) = 0 |
|
Solving for z then produces the functional form z = y-x.
Finally, since r×( u×v)
is orthogonal to u×v, the vector r×( u×v) must be in the span of u and v. That is, there must be scalars a and b such that r×(u×v) = au+bv.
Also, since r×( u×v) is orthogonal to r, we have
|
r·( au+bv) = 0 or ar·u = -br·v |
|
Indeed, it is straightforward to show that a = r·v and b = -r·u , thus leading to the triple vector product identity:
|
r×( u×v) = ( r·v) u-( r·u) v |
| (4) |
Exercises 41-44 will provide additional insights into the interpretation and
application of (4).
EXAMPLE 8 Verify (4) for the vectors
|
u =
á 1,2,0
ñ , v =
á1,1,0
ñ , and r =
á 3,2,1
ñ |
|
Solution: Since u×v =
á0,0,-1
ñ , the left side of (4) is
|
r×( u×v) =
á3,2,1
ñ ×
á 0,0,-1
ñ =
á-2,3,0
ñ |
|
Notice that u, v, and r×( u×v) are parallel to the xy-plane. The right side of (4) is
|
|
|
|
(
á 3,2,1
ñ ·
á1,1,0
ñ ) u-(
á3,2,1
ñ ·
á 1,2,0
ñ ) v |
| |
|
| |
|
| |
|
| |
|
|
|

