Part 2: Equation of a Plane
Given any plane, there must be at least one nonzero vector n =
á a,b,c
ñ that is perpendicular to every
vector v parallel to the plane.
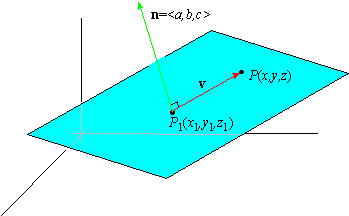
In particular, the plane through the point P1(x1,y1,z1) with normal vector n =
áa,b,c
ñ is the set of points P(x,y,z) such that
the vectors
|
 |
|
|
v = |
P1P |
=
áx-x1,y-y1,z-z1
ñ |
|
are perpendicular to n. However,
n·v = 0 is equivalent to
|
á a,b,c
ñ ·
á x-x1, y-y1, z-z1
ñ = 0 |
|
Computing the inner product then leads us to the following definition:
Definition 4.3: The equation of the plane with normal n =
á a,b,c
ñ through the point
áx1,y1,z1
ñ is
|
a( x-x1) +b( y-y1) +c( z-z1) = 0 |
| (2) |
If c ¹ 0, then we can transform (2) into functional form, which is
where m = -a/c, n = -b/c and d = ( ax1+by1+cz1) /c.
EXAMPLE 3 Find the equation of the plane with normal n =
á 1,2,7
ñ which contains the point P1(5,3,4).
Solution: To do so, we substitute into the equation (2). The result is that
|
1( x-5) +2( y-3) +7( z-4) = 0 |
|
We then solve for z to obtain the functional form:
To find the equation of the plane through three non-collinear
points P1, P2, and P3, we first form the two vectors
|
 |
|
 |
| u = |
P1P2 |
and v = |
P1P3 |
|
Since u and v are both parallel to the plane, the
cross product u×v must be perpendicular to the plane.
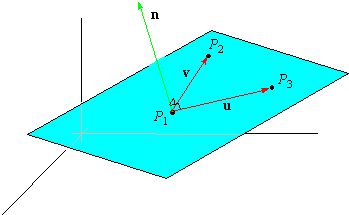
We use Definition 4.3 with n = u×v to write the equation of the plane.
EXAMPLE 4 Find the equation of the plane passing through P1( 1,2,2) , P2( 4,6,1) and P3(0,5,4) .
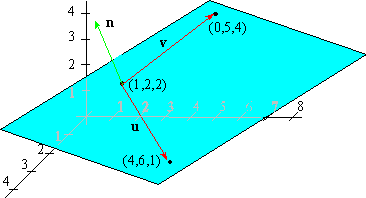
Solution: We form the vectors
|
 |
|
| u = |
P1P2 |
=
á4-1,6-2,1-2
ñ =
á 3,4,-1
ñ |
|
 |
|
| v = |
P1P3 |
=
á0-1,5-2,4-2
ñ =
á -1,3,2
ñ |
|
The cross product of u and v is
Thus, the equation of the plane through P1, P2, and P3 is
|
11( x-1) -5( y-2) +13( z-2) = 0 |
|
which in functional form is
Check your Reading: Explain why P2(1,2,2) satisfies (3).



