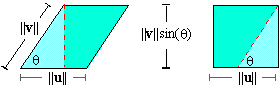Part 3: Parallelograms and Triangles

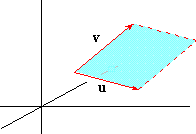
Given two vectors u and v with a common initial point, the set of terminal points of the vectors su+tv for 0 £ s,t £ 1 is defined to be parallelogram spanned by u and v.  
We can explore the parallelogram spanned by two vectors in a 2-dimensional coordinate system. That is, because coordinate systems are a figment of our collective imaginations, we can imagine the parallelogram spanned by two vectors as being in an x' y' coordinate system, where the x'-axis is parallel to u and the y'-axis is in the same plane as u and v.   

(Click and drag arrow's endpoint. Angles are in degrees.)

Since u = || u || i and v = || v|| ( cos( q) i + sin( q) j) in the x' y' coordinate system, their cross product is

u×v = || u||  || v||  ( cos( q) i×i + sin( q) i×j) = || u||  || v||  sin( q) k

This results in the following theorem:       

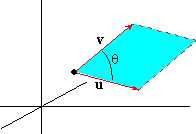
Theorem 3.3: If q is the angle formed by u and v, then

|| u×v|| = || u|| || v|| sin(q)

       

Let 's consider two applications of Theorem 3.3.  First, if u and v are parallel, then q = 0 and u×v = 0. Second, the parallelogram spanned by u and v can be cut into two parts which form a rectangle with height || v|| sin( q) and base || u|| ,

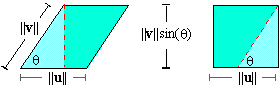
Thus, the area of the parallelogram formed by u and v is || u|||| v|| sin( q) . Indeed, we have the following:

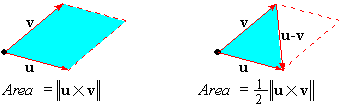
The latter result follows from the fact that u-v bisects the parallelogram formed by u and v.

       

EXAMPLE 5    Find the area of the triangle with vertices at P₁( 2,2) , P₂( 4,4) , and P₃(6,1) .

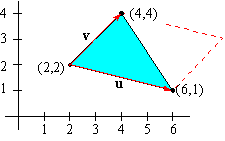
Solution: It is easy to see that u = á2,2 ñ and v = á 4,-1 ñ . As vectors in R³, we have u = á2,2,0 ñ and v = á 4,-1,0 ñ . Thus, their cross product is

u×v = 2 0 4 0 , 0 2 0 -1 , 2 2 4 -1 = á 0,0,  2·( -1) -4·2   ñ = á 0,0,-10 ñ

Since the triangle has half of the area of the parallelogram formed by u and v, the area of the triangle is

Area = || u×v|| =   1 2 02+02+(-10) 2   = 5  units2

       

EXAMPLE 6    Find the area of the triangle with vertices P₁( 3,0,2) , P₂( 4,6,1) , and P₃(0,5,4) .

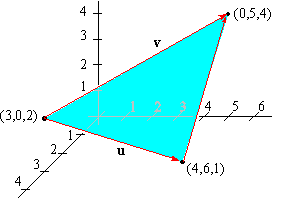
Solution: To do so, we first construct the vectors u and v:

u  =   P1P2   = á4-3,6-0,1-2 ñ = á 1,6,-1 ñ v  =  P1P3   = á0-3,5-0,4-2 ñ = á -3,5,2 ñ

As vectors in R³, we now have u = á2,2,0 ñ and v = á 4,-1,0 ñ . Thus, their cross product is

u×v = 6 -1 5 2 , -1 1 2 -3 , 1 6 -3 5 = á 6·2-5·( -1) ,( -1) ·( -3) -2·1,1·5-( -3) ·6 ñ = á 17,1,23 ñ

Since the triangle has half of the area of the parallelogram formed by u and v, the area of the triangle is

Area = || u×v|| =   1 2 172+22+232   = 14.335  units2

Maple/Javaview Figure