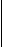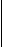Part 2: The Triple Scalar Product

If r = á r₁,r₂,r₃ ñ , u = á u₁,u₂,u₃ ñ , and v = á v₁,v₂,v₃ ñ , then (3) implies that

r · ( u×v) = r1 r2 r3 u1 u2 u3 v1 v2 v3

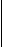
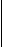
However, by (4) we have
We call this identity the triple scalar product:

r · ( u×v)  =  ( r×u) · v

The triple scalar product is often used to obtain other properties of the cross product. For example, u×u = 0 implies that

u · ( u×v) = ( u×u) · v = 0

Since v · ( u×v) = -v · ( v×u) , the same calculation shows that that u×v is orthogonal to v.        

Theorem 3.2: u×v is orthogonal to u and to v.       

That is, (u×v) ^ u and (u×v) ^ v .

EXAMPLE 3    Show that u×v is orthogonal to u when u = á 2,3,7 ñ and v = á 1,4,2 ñ .       

Solution: To begin with, let us notice that

u×v = 3 7 4 2 ,   7 2 2 1 ,   2 3 1 4 = á 6-28, 7-4, 8-3 ñ = á -22, 3, 5 ñ

Now let's compute u · ( u×v) :

u·( u×v) = á2,3,7 ñ · á -22,3,5 ñ = -44+9+35 = 0

Vectors u, v, and u×v are shown below:

Maple/javaview image

As another example, consider that

i×j =    0 0 1 0  , 0 1 0 0 , 1 0 0 1 = á 0,0,1 ñ

That is, i×j = k, which is perpendicular to both i and j. Indeed, it can be shown that

i×j = k j×i = -k i×i = 0 j×k = i k×j = -i j×j = 0 k×i = j i×k = -j k×k = 0

(5)

The identities (5) can be memorized using the mnemonic below:
That is, the cross product of any two vertices is the third vertex, with the sign determined by the implied direction (positive if counterclockwise, negative otherwise).       

EXAMPLE 4    Evaluate u×v when u = i-2j and v = j+k. Then show that ( u×v) ^ u and ( u×v) ^ v        

Solution: To begin with, we use property iii):

u×v = ( i-2j) ×( j+k) = i×( j+k) -2j×( j+k) = i×j+i×k-2j×j-2j×k

We then use table (5) to finish the computation:

u×v = k-j-2·0-2i = -2i-j+k

Notice that u·( u×v) = 1(-2) -2( -1) = 0 and

v · ( u×v) = 1( -1)-1( 1) = 0