Exercises

Compute  u×v and  v×u.  Also, show that u and v are orthogonal to u×v.
1.
u = á 2,1,0 ñ , v = á3,1,0 ñ
2.
u = á 2,1,0 ñ ,v = á -1,3,0 ñ
3.
u = á 3,3,0 ñ , v = á2,0,0 ñ
4.
u = á 0,1,0 ñ ,v = á 0,0,1 ñ
5.
u = á 1,0,0 ñ , v = á0,1,0 ñ
6.
u = á 1,0,0 ñ ,v = á 1,0,0 ñ
7.
u = á 2,3,7 ñ , v = á7,3,5 ñ
8.
u = á 6,2,9 ñ ,v = á 1,0,3 ñ
9.
u = á 3,4,2 ñ , v = á9,12,6 ñ
10.
u = á 1,1,1 ñ, v = á -1,-1,-1 ñ

Sketch the triangle formed by the three points P1, P2 and P3 and then find its area.
11.
P1( 0,0) , P2( 1,2) , P3(2,1)
12.
P1( 0,0) , P2( 2,3) ,P3( 1,1)
13.
P1( 1,3) , P2( -2,5) , P3(2,1)
14.
P1( -1,4) , P2( 3,4), P3( 0,-3)
15.
P1( 1,0,0) , P2( 0,1,0) , P3(0,0,1)
16.
P1( 0,0,0) , P2(1,1,0) , P3( 1,1,1)
17.
P1( 0,0,0) , P2( 1,2,1) , P3(2,1,2)
18.
P1( 1,3,2) , P2(2,7,9) , P3( 2,1,5)
 

Sketch the parallelepiped spanned by u, v, and w assuming all vectors have initial points at the origin.  Then calculate the volume of the parallelepiped.
19.
u = á 2,0,0 ñ , v = á 1,2,0 ñ , w = á0,0,3 ñ
20.
u = á 1,0,0 ñ , v = á 1,1,0 ñ ,  w = á1,1,1 ñ
21.
u = á 2,0,0 ñ , v = á 0,2,0 ñ , w = á1,1,1 ñ
22.
u = á -1,2,0 ñ, v = á 2,1,0 ñ ,  w = á1,3,2 ñ
23.
u = i+k, v = 2j-k,  w = j+2k
24.
u = i+j, v = j+k,  w = k+i
25.
u = á l,0,0 ñ , v = á 0,w,0 ñ , w = á0,0,h ñ
26.
u = á l,0,0 ñ ,  
v =
 l
Ö2
 ,  l
Ö2
 ,0
, w =
0,  l
Ö2
 ,  l
Ö2
 

27. Let u =  áu1,u2,u3 ñ and let v = áv1,v2,v3 ñ . Use (2) to show that v×u is the same as -( u×v) .

28. Show that
|| u×v ||2 = || u ||2  ||v||2 - ( u·v) 2

 29. Let u =  áu1,u2,u3 ñ , v = áv1,v2,v3 ñ , and a = áa1,a2,a3 ñ . Show that
a×( u+v) = a×u+a×v

30. Let u =    áu1,u2,u3 ñ and v = áv1,v2,v3 ñ , and let k be a number. Show that
k( u×v) = ( ku) ×v       and       k( u×v) = u×( kv)

31.  Use the x' y' coordinate system to show that if u and v are 3-dimensional vectors, then u · v  = ||u|| ||v|| cos(q).  How would you use projections to define the y'-axis in the x' y' coordinate system?
(Click and drag arrow endpoints.)

32.  Let u and v be in the polar forms (in the x' y' coordinate system in exercise 31) given by
u = á ||u|| cos( a) ,||u|| sin( a), 0 ñ
v = á ||v|| cos( b) ,||v|| sin( b), 0 ñ
        
Show that || u×v || = ||u|| ||v|| sin(q)  where q = b-a.

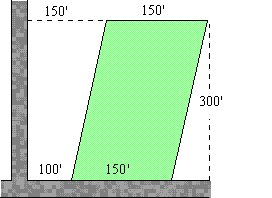
33.  Jane buys a lot that is 150 feet wide across the front and back, and the back right corner is 300 feet along a perpendicular from the road fronting the property.  The front left corner is 100 feet from a road which intersects the fronting road at a right angle, and the back left corner is 150 feet from that same road.

What is the area of Jane's lot in acres? (Hint: 1 acre = 43,560 feet2).

34.  Roy intended to pour a 24¢ by 16¢ rectangular concrete patio, but he didn't check closely for square and instead ended up with a deck in the form shown below


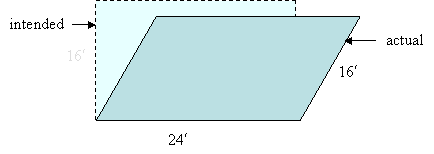
Which has more area, the patio Roy intended to build or the one he ended up with?

35. Write to Learn: Write a short essay in which you develop the area formula for a triangle whose vertices have coordinates ( x1,y1) , ( x2,y2) , and (x3,y3) , respectively. Write the essay as if you were instructing a group of surveyors.

36. Write to Learn: Suppose s denotes the length of a side of a regular hexagon.
Write a short essay deriving and explaining a formula for the area of a hexagon as a function of s.

37. Sketch the parallelepiped spanned by u = á 1,0,0 ñ , v = á1,1,0 ñ , and w = á 0,0,1 ñ assuming that all vectors have initial points at the origin.

  1. Calculate the volume of the parallelepiped using Volume = | u·( v×w) | .

  2. Calculate the volume of the parallelepiped using Volume = |( u×v) ·w| .  Why should you expect the same result as in (a)?

  3. How might you have obtained the result by slicing and rearranging"?

38.  Sketch the parallelepiped spanned by u = á 2,0,0 ñ , v = á0,2,0 ñ , and w = á 1,1,1 ñ assuming that all vectors have initial points at the origin.  

  1. Calculate the volume of the parallelepiped using Volume = | u·( v×w) | .

  2. Calculate the volume of the parallelepiped using Volume = |( u×v) ·w| .  Why should you expect the same result as in (a)? 

39.  Write to Learn: Suppose that over a short period of time, dt, a rectangle in the xy-plane with length dx and width dy moves from the initial point to the terminal point of a vector v = á a dt, b dt, c dt ñ , where a, b, and c are numbers.
Click image to toggle animation.
Write a short essay deriving a formula for the volume of the parallelepiped swept out by the rectangle over that short time period.

40.  What is the volume of the prism shown in the figure below?

 

Exercises 41 - 48 explore the important application of rotation of a vector about a given axis.

41.  If u is orthogonal to a unit vector n, then we define u^, pronounced "u perp," to be  
u^ = n × u
Explain why u^ and u are orthogonal and have the same length.  (Note: u^ is a 90° rotation of the vector u about a line or axis parallel to n ).

Maple/javaview image

42.  What is the vector u^ obtained by rotating u = á a,b ñ through an angle of 90° about the z-axis.

43.  Suppose that u is orthogonal to a unit vector n and that
uq = cos(q) u+sin(q) u^

where  u^ = n×u (See exercise 41).

Maple/javaview image

In (a) - (c) below, we will show that uq is the rotation of u through an angle of q about an axis parallel to n.
  1. Explain why uq is orthogonal to n.  
  2. Show that ||uq|| = ||u|| (Hint: calculate uq · uq )
  3. Show that q is the angle between uq and u.

44. Use the result in exercise 43 to obtain uq when u = á a,b,0 ñ is rotated about the z-axis.   

45. In this exercise, we develop a formula for vq, which is the vector obtained by rotating a vector v about a unit vector n.

Maple/javaview image

As the image above shows, the key is to decompose v into the sum of a vector projn( v) parallel to n and a vector u that is orthogonal to n.  In fact, u is rotated about n to produce uq, and then uq is combined with projn(v) to produce vq. 
  1. Show that projn( v) = ( v·n) n and let u = v - projn( v) .  Notice that
    v = u + projn( v)
  2. Let vq be the vector obtained by rotating v through an angle q about n.  Use the figure to explain motivate the definition
    vq = uq + projn( v)
  3. Use the definitions and exercise 43 to show that
    vq = cos( q) u + sin(q) ( n×u) + ( v·n) n

46.  Let's show that the formula in exercise 45(c) is valid.

  1. Explain why if n, vq and v have a common initial point, then the endpoints of vq and v are on a circle perpendicular to and centered on an axis parallel to n.  Also, explain why q is the angle between the two endpoints of vq and v on this circle.
  2. Show that ||vq|| = ||v|| (Hint: calculate vq·vq )
  3. Show that v and vq form identical angles with n.

47.  Use 45c to obtain the general formula for rotating a vector v = á a,b,c ñ about the z-axis.

48.  Write to Learn:  For fixed n and q, the transformation from v to vq  is a linear transformation, which means that it transforms sums and scalars of vectors to sums and scalars of the transformed vectors.  Write a short essay demonstrating the linearity of the transformation in 45(c) by showing that if v and w are vectors and a,b are scalars, then av+bw  is rotated to the vector avq+bwq.