Exercises

Sketch the two vectors. Then find the length of each of the two vectors and their direction. Finally, use (1) to find the angle between them.

1. u = á 3,4 ñ ,  v = á0,2 ñ 2. u = á 5,12 ñ ,  v = á 5,0 ñ 3. u = á -1,5 ñ ,  v = á2,9 ñ 4. u = á 1,11 ñ ,  v = á 3,8 ñ 5. u = á 6,8 ñ ,  v = á8,-6 ñ 6. u = á 3,4 ñ ,  v = á 6,8 ñ 7. u = á 2,2,1 ñ ,  v = á6,0,2 ñ 8. u = á 3,1,4 ñ,  v = á 2,0,2 ñ 9. u = á 0,0,1 ñ ,  v = á1,0,0 ñ 10. u = á 0,0,1 ñ,  v = á 2,0,2 ñ

Find the value(s) of the parameter k for which the two vectors are orthogonal.

11. u = á 2,k ñ ,  v = á6,1 ñ 12. u = á k,7 ñ ,  v = á -1,5 ñ 13. u = á 3,1,2 ñ ,  v = á-2,k,2 ñ 14. u = á 0,2,1 ñ,  v = á 6,k,2 ñ 15. u = á k,2,k ñ ,  v = ák,-3,1 ñ 16. u = á0.2,3k,1 ñ ,  v = á 6,9.1,2 ñ 17. u = á -0.1,-2.3,7.5 ñ ,  v = á 2.3,3.5,k ñ 18. u = á0.2,3k,1 ñ ,  v = á 6,9.1,2 ñ

Find the projection of the vector v onto the vector p.  Then show that

w = v-projp( v)

is perpendicular to p.

19. p = á 1,7 ñ ,  v = á2,11 ñ 20. p = á 3,4 ñ ,  v = á 7,4 ñ 21. p = á 1,2,1 ñ ,  v = á2,2,7 ñ 22. p = á 3,5,9 ñ,  v = á 2,11,6 ñ 23. p = j, v = 2i-3j+4k 24. p = k, v = 2i-3j+4k

Find the direction cosines and direction angles for the following vectors.

25. v = á 1,Ö3 ñ 26. v = á Ö3,Ö3 ñ 27. v = á Ö2,Ö2,2 ñ 28. v = á 1,Ö2,1 ñ 29. v = á 1,0,1 ñ 30. v = á 1,Ö3,0 ñ

31. Find a 2-dimensional unit vector u which forms an angle of 30^° with the vector v = á3,4 ñ .

32. Find a 2-dimensional vector u with length 4 which forms an angle of 135^° with the vector v = á 4,1 ñ .

33. Is there a value of k such that u = á 3,0,2 ñ   is perpendicular to v = á -2,k,2 ñ ? Can you explain geometrically why v cannot be perpendicular to u for any value of k?

34. Find the projection of the vector v = á 3,1,4 ñ onto the vector p = á2,-10,1 ñ . Explain.

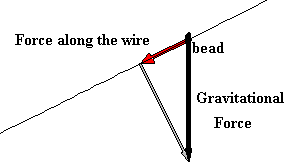
35. A frictionless bead of mass 1 kg slides down a wire which is parallel to the vector v = á 2,1 ñ .
Find proj_v( F_g) , which is the part of the gravitational force in the direction of motion of the bead. (Hint: use -9.8 m/sec² for the acceleration due to gravity near the earth's surface).

36. Repeat exercise 35 if v forms an angle of 30^° with the horizontal.

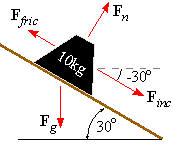
37. A 10 kg block is initially at rest on a board with a coefficient of static friction of m_s = 0.2 between them. The board runs 7 feet horizontally and rises 3 feet vertically. The force of gravity is F_g = á0,-98 ñ  (i.e., product of the mass and an acceleration of -9.8 m/sec² ).
The force parallel to the incline is F_inc ,  which is the projection of F_g onto the vector <7,3> that is parallel to the board.  The force normal F_n is perpendicular to F_inc .  Specifically, F_n  is the negative of

w = Fg-Finc

Finally, the force of static friction is the force in the opposite direction of F_inc with a magnitude of m_s ||F_n|| (that is,

Ffric = -ms  ||Fn||  Finc ||Finc||

What are F_inc, F_n, and F_fric?

38. The block in exercise 37 will begin to slide if || F_inc|| ³  m_s || F_n|| . Does this block begin to slide? 

39. Repeat exercises 37 and 38 for the block shown below left:

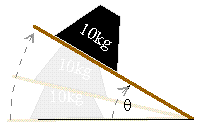Exercise 39     Exercise 40

40.  Suppose a board with a coefficient of static friction of m_s = 0.2 is lifted from horizontal as shown above right.  Use exercise 38 to determine the angle q at which the block begins to slide down the board? (Note: this is also a method for measuring  m_s ). 

41. Use the properties of the inner product to show that

|| u+v||2 = || u||2  + 2u·v + || v||2

42. Use the properties of the inner product to show that

|| u-v||2 = || u||2 - 2u·v + || v||2

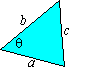
and then use the result to prove the law of cosines,

c2 = a2+b2-2abcos( q)

43.  Substitute the vectors u = áu₁,u₂,u₃ ñ and v = áv₁,v₂,v₃ ñ into the following identities to prove that they are true.

i) u·v = v·u ii) ( ku) ·v = k( u·v) = u·( kv) iii) u·( v+w) = u·v+u·w iv) v·v ³ 0 and v·v = 0 only if v = 0

44. We call u · v = u₁v₁+u₂v₂+u₃v₃ the standard inner product because it is possible to define other inner products. Indeed, show that if u = áu₁,u₂,u₃ ñ and v = áv₁,v₂,v₃ ñ , then

u ◦ v = 3u1v1+4u2v2+5u3v3

also satisfies the properties in Theorem 2.1.

45. Let v = á a,b,c ñ and let k be a scalar.

1. Compute || kv|| .
2. Show that the result in (a) reduces to | k| || v|| .

46. Let u and v be vectors.

1. Explain why 2u·v £ 2|| u||  || v|| .
2. Use (a) and the result in problem 45 to show that

   || u+v||2  £  || u||2  +  2|| u||  || v||  +  || v||2

   and then explain why this implies the triangle inequality || u+v||  £  ||u|| + ||v|| .

47. What are the angles between a diagonal of a cube and the edges of the cube it is adjacent to? (i.e., the brown and green edges in the figure below)

48. Suppose we have a pyramid whose base is a square and whose sides are equilateral triangles.
What is the angle between an edge of a triangle and an adjacent diagonal of the base?