Part 4: Free Body Diagrams

A force acting on a body (i.e., object) is represented mathematically by a vector. A force diagram, which is also known as a free body diagram, is a sketch in which all the force vectors acting on an object are drawn with their initial points at the location of the object.

A force F acting on a body (i.e., object) is represented mathematically by a vector, in that it has a magnitude ||F|| which is applied in a given direction.  The magnitude ||F|| is measured in Newtons, where 1 Newton is the force required to accelerate a 1 kg mass at a rate of 1 meter per second per second (i.e, 1 N = 1 kg·m/sec² ).  

A force diagram, which is also known as a free body diagram, is a sketch in which all the force vectors acting on an object are drawn with their initial points at the location of the object.  The net force acting on the body is the sum of all the forces in the force diagram.

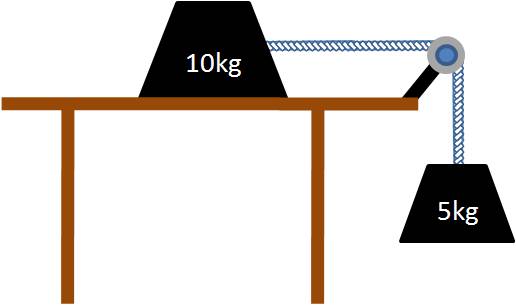
EXAMPLE 8    A 10kg block resting on a table is attached by a "massless" rope to a 5 kg block hanging off the end (with the rope running across a "frictionless" pulley).

Draw the free-body diagram and determine the net force if the 10kg block is experiencing a force of friction with a magnitude of 30 newtons.    

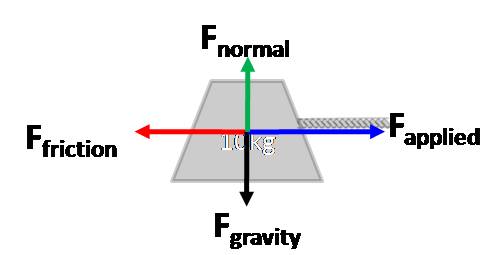
Solution: To begin with, the force of gravity F_gravity is pulling the 10 kg block toward the earth, which via Newton's third law is countered by a force normal (i.e., perpendicular) to the table that resists the 10 kg blocks fall. If the block is not moving vertically, then F_normal and F_gravity must have the same magnitude so that they cancel each other out (i.e, no net force up or down).    Using Newton's law F = ma, we can show that the 5kg block is subject to a gravitational force of

F5kg = 5kg·  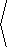   0,-9.8 m sec2  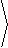=  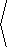 0,-49 m sec2

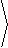Since ||F_5kg|| = 49N, the 5kg block applies a force of

Fapplied = 49i  Newtons

to the 10kg block. Finally, the force of friction F_friction resists the horizontal motion of the block, so it is applied in the direction -i, or

Ffriction = -30i Newtons

Thus, the net force is

Fnet  =   Fgravity+Fnormal+Fapplied+Ffriction   = 0+49i-30i   = 19i

In example 8, a net force of F_net = 19i means that the 10kg block is accelerating to the right at a rate of 1.9 meters per second per second.  In contrast, had the friction had a magnitude of 49 Newtons, it would not be moving at all - i.e., it would be at rest with the 5kg block likewise at rest as it hangs suspended in midair.

If the net force acting on a body is 0, then the body is said to be at equilibrium. When it occurs, equilibrium often can be used to determine unknown quantities in a free body diagram.

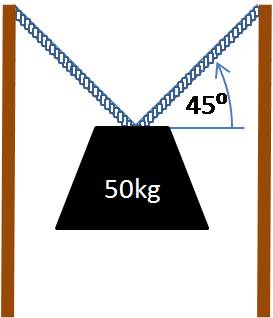
EXAMPLE 9    A 50kg block is suspended by 2 identical cables of the same length forming 45^° angles with the horizontal.

If the block remains motionless over time, then what is the magnitude of the tensile force exerted by each of the cables on the block?   Solution:  In this case, the free body diagram of the 50 kg mass is given by the figure below. The force of gravity is

Fgravity = 50kg· á 0,-9.8  m / sec2 ñ = á 0,-490N ñ

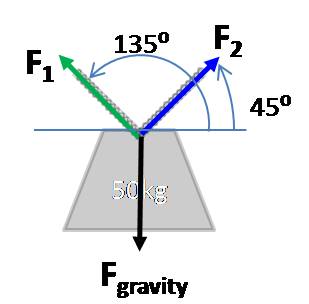
If we let F denote the (unknown) magnitude of the force exerted by a cable, then

F1 = F  á cos(135° ) , sin(135° ) ñ =  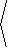- FÖ2 ,  FÖ2  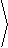 F2 = F  á cos(45° ),  sin(45° ) ñ =   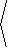F Ö2 ,  FÖ2

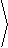Consequently, the net force is

Fnet   = Fgravity+F2+F1     = á 0,-490 ñ +  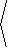   F Ö2 ,  FÖ2 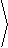+  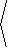- F Ö2  ,     F Ö2  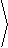     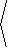= 0,-490+   2F Ö2

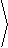Since F_net = 0 (equilibrium), we have

2 F Ö2 = 490,  F=    490Ö2 2    =  346.48 N